Intro to Algos - 25
Welcome to the Lemonade Time,
1. Intro to Algorithms - with Pseudo / pseudḗs Codes
1. Simple Methods - Roughly n^2 Comparisons
- Bubble Sort - Push Max to the right - Best time = O(n)
for i = n to 2 do
for j = 2 to i do
if A[j] < A[j - 1] then
t = A[j]
A[j] = A[j - 1]
A[j - 1] = t
- Select Sort - Find Min to the left - Best time = O(n^2)
for i = 1 to n - 1 do
k = i
for j = i + 1 to n do
if A[j] < A[k] then
k = j
exchange A[i] and A[k]
- Insetion Sort - Insert Current into Sorted Left - Best time = O(n)
for i = 2 to n do
j = i - 1
t = A[i]
while j ≥ 1 ∧ t < A[j] do
A[j + 1] = A[j]
j = j - 1
A[j + 1] = t
2. Fast Methods - Roughly n*log(n) Comparisons
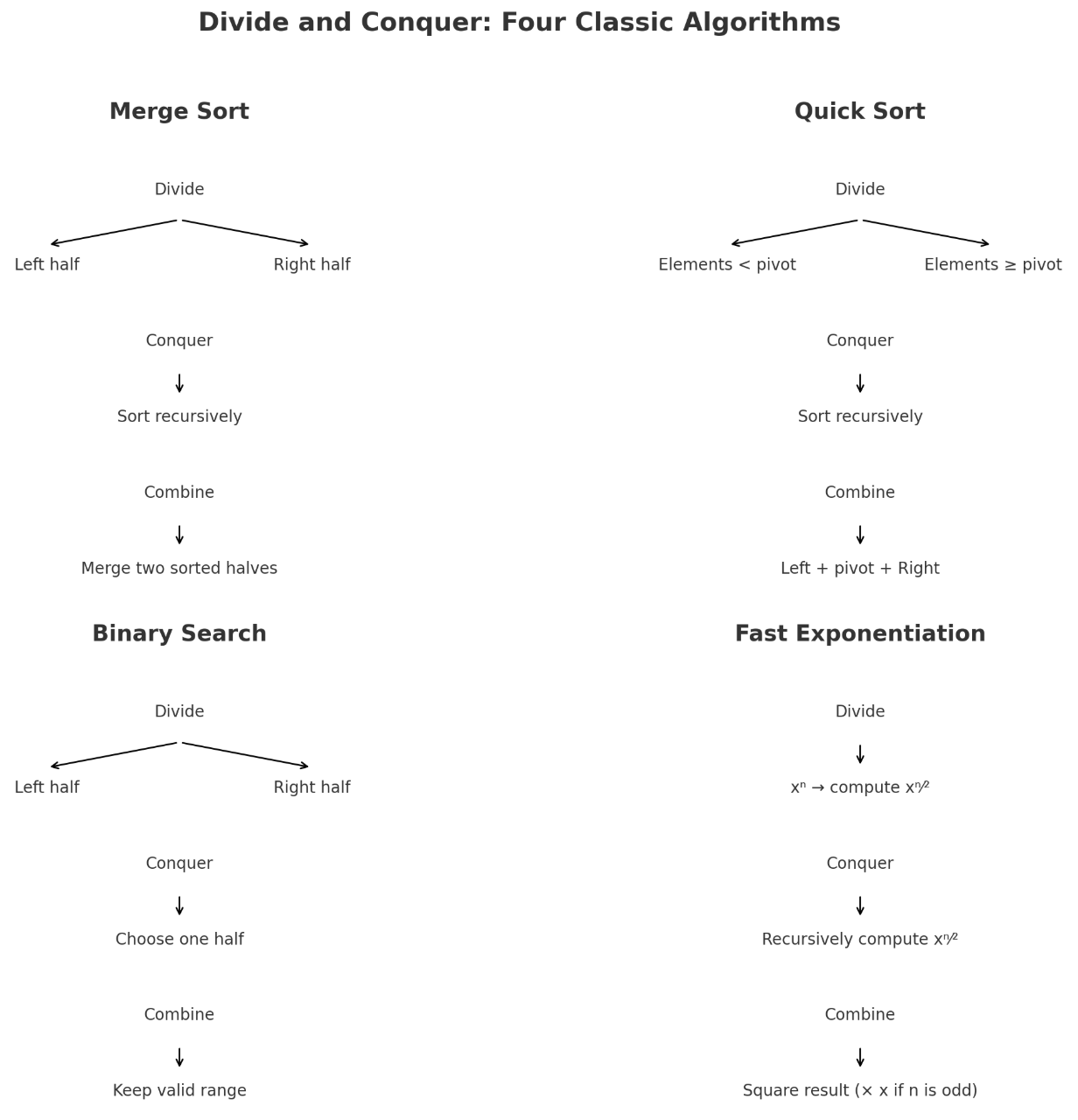
- Merge Sort
if length(A) ≤ 1 then
return A
mid ← length(A) // 2
left ← MergeSort(A[0 : mid])
right ← MergeSort(A[mid : ])
return Merge(left, right)
- Heap Sort
n ← length(A)
// Step 1: Build Max Heap
for i = n / 2 downto 1 do
Heapify(A, i, n)
// Step 2: Extract elements one by one
for i = n downto 2 do
swap A[1], A[i]
Heapify(A, 1, i - 1)
- Quick Sort
if low < high then
pivot_index ← Partition(A, low, high)
QuickSort(A, low, pivot_index - 1)
QuickSort(A, pivot_index + 1, high)
Sieve of Eratosthenes
- ALGORITHM SieveOfEratosthenes(n)
- INPUT: n – upper limit to find primes
- OUTPUT: list of all prime numbers from 2 to n
1. Initialize array
CREATE boolean array is_prime[0..n]
FOR i = 0 TO n DO
SET is_prime[i] = TRUE
END FOR
SET is_prime[0] = FALSE
SET is_prime[1] = FALSE
2. Sieve
FOR i = 2 TO floor(sqrt(n)) DO
IF is_prime[i] = TRUE THEN
// Mark multiples of i as composite
FOR j = i * i TO n STEP i DO
SET is_prime[j] = FALSE
END FOR
END IF
END FOR
3. Collect primes
CREATE empty list primes
FOR i = 2 TO n DO
IF is_prime[i] = TRUE THEN
ADD i TO primes
END IF
END FOR
RETURN primes
Hilbert Curve - Hi is the Hilbert curve of order i
Procedure DrawHilbert(x, y, size, depth, direction):
if depth == 0 then return
Rotate direction as needed
Recursive call:
DrawHilbert(lower left, depth - 1, new direction)
Draw line to lower right
DrawHilbert(lower right, depth - 1, same direction)
Draw line to upper right
DrawHilbert(upper right, depth - 1, same direction)
Draw line to upper left
DrawHilbert(upper left, depth - 1, rotated direction)
Merge Sort
Tromino Tiling
Heapify
2. Recursion
Draw a Sierpinski triangle
- The algorithm uses divide-and-conquer logic
- The number of triangles grows as 3^d, where 𝑑 is the depth
- At depth 0, the drawing terminates (base case)
- The shape is self-similar: each part looks like the whole
Algorithm SierpinskiTriangle(vertices, depth):
Input:
vertices: list of 3 points defining a triangle (A, B, C)
depth: recursion depth
if depth == 0 then
DrawTriangle(vertices)
else
A, B, C ← vertices
AB ← midpoint between A and B
BC ← midpoint between B and C
CA ← midpoint between C and A
SierpinskiTriangle([A, AB, CA], depth - 1) // Top-left triangle
SierpinskiTriangle([AB, B, BC], depth - 1) // Top-right triangle
SierpinskiTriangle([CA, BC, C], depth - 1) // Bottom triangle
3. Dynamic Data Structures + Abstract Data Types
Hash functions
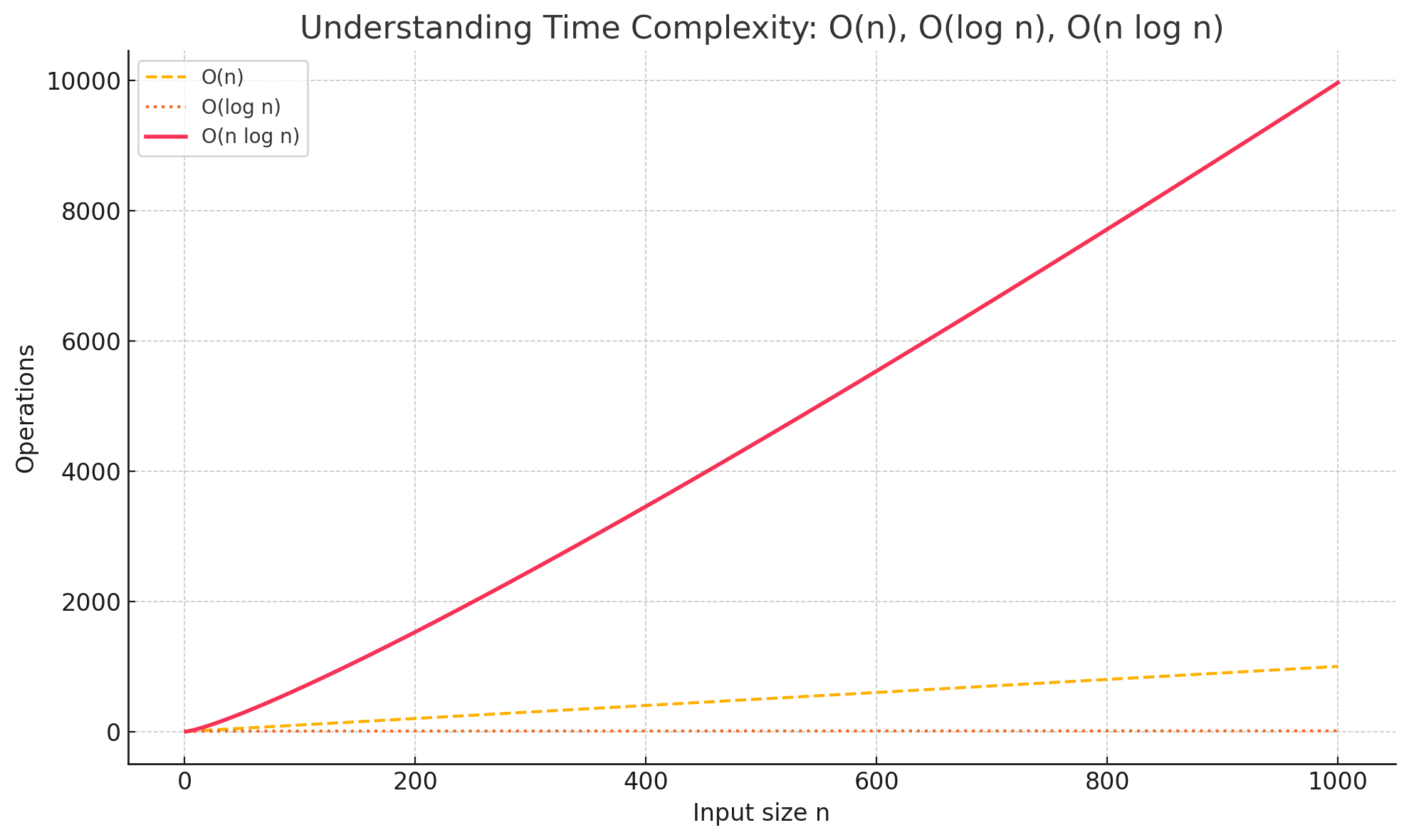
Some Other Time Complexity
| Algorithm | Time Complexity |
|---|---|
| Binary Search | O(log n) |
| Insertion Sort | O(n²) |
| Merge Sort | O(n log n) |
| Traveling Salesman (Brute) | O(n!) |
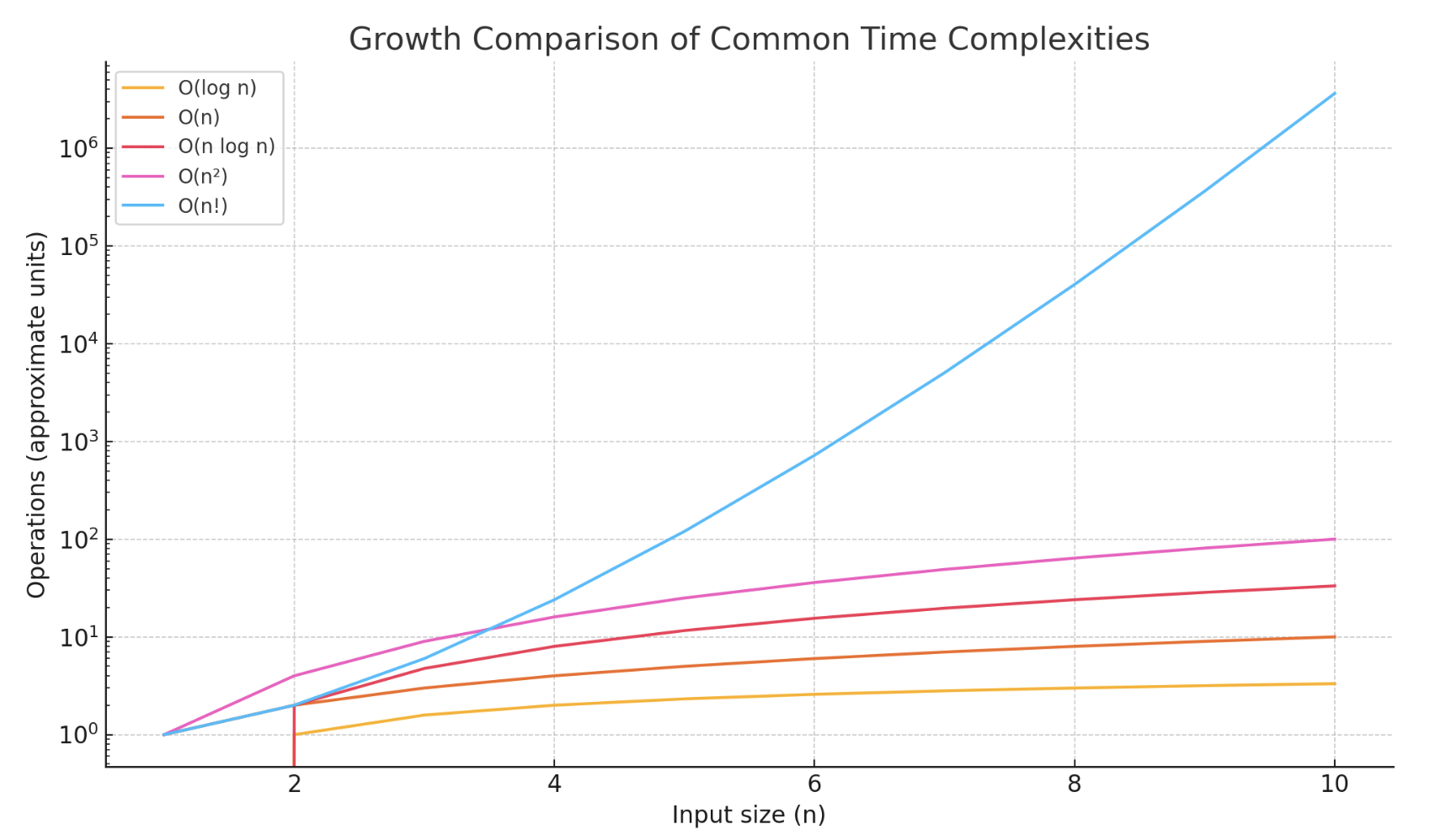
Try to keep the time complexity within O(n log n)
If your algorithm approaches O(n²) or worse, Consider Applying,
- Divide and Conquer
- State Compression
- Pruning techniques
- Or look for a better Algorithm
4. Collision Resolution
5. Dynamic Programming
Design techniques
Fibonacci numbers
Matrix multiplication
Longest common subsequence, coin changing
Enjoy Reading This Article?
Here are some more articles you might like to read next: