Background Readings
Model Sharding
| Aspect | JAX Sharding | PyTorch Sharding | Programming Language Analogy |
| User Experience | More intuitive and declarative | Less intuitive, more imperative | Python > C++ |
| Expressiveness Constraints | Strongly constrained | Weakly constrained | Python > C++ |
| Extensibility | Closed design | Open design | C++ > Python |
| Ability to Represent Irregular Cases | Limited | Strong | C++ > Python |
| Tolerance for “Ugly but Useful” Solutions | Not allowed | Allowed | C++ |
Logits and Labels
Starting from Geoffrey Hinton, Oriol Vinyals, Jeff Dean, 2015. and previous work
- Knowledge is not parameters, but the mapping from
Input to Output Distributions
Previously: logits ≈ regression target
After Distilling the Knowledge in a Neural Network 2015: soft label ≈ probability geometry
3 Stages of Training Config
- KD → representation alignment → conditional LM fine-tuning
- In Stage III, after freezing the encoder, we linearly decay the
contrastive loss weight to 0.1, as its contribution to representation learning diminishes and may introduce misaligned gradients during decoder optimization
check
"final_ce": history["ce"][-1] if len(history.get("ce", [])) > 0 else None,
"final_kl": history["kl"][-1] if len(history.get("kl", [])) > 0 else None,
"final_geo": history["geo"][-1] if len(history.get("geo", [])) > 0 else None,
"final_contrastive": history["contrastive"][-1] if len(history.get("contrastive", [])) > 0 else None,
LoRA + Freezing Parameters: Optimizer Caveat
- The optimizer still holds state (e.g., AdamW momentum) for the frozen parameters, these parameters:
- are not updated, but their optimizer states remain inactive (“stale”)
import librosa
from jiwer import wer, cer, CharacterErrorRate
Diffusion Models
def compute_distillation_loss()
cos_sim = (s * t).sum(dim=-1).clamp(-1 + eps, 1 - eps)
geo_loss = torch.acos(cos_sim).mean()
...
total_loss = ()
return total_loss, ce_loss.item(), kl_loss.item(), geo_loss.item()
- [1/3] Stabilizing the Training, in Latent Space
- [2/3] Training Loss with different training set amounts
Italian MLS dataset
Dataset: 59623 files x 4 epochs = 238492 samples
Dev: 1248 transcripts, 1248 files
Optimization and Scheduling
| Component | Your Configuration |
| Optimizer | AdamW |
| Weight decay | 0.01 |
| Scheduler | CosineAnnealingLR |
| Max steps | 20,000 |
| Min LR | 1e-6 |
| Mixed precision | AMP (fp16) with GradScaler |
| Gradient clipping | Global norm = 1.0 |
Training set: 59,623 audio–text pairs
Development (validation) set: 1,248
Test set: 1,262
Batch size: 64
Total training steps (MAX_STEPS): 8,000
Equivalent number of epochs: ≈ 4
Initialization and State Management
| Component | Initialization |
| Teacher | Fully pretrained, frozen |
| Student backbone | Pretrained Whisper-medium |
| LoRA adapters | Random init (rank=xxx), trainable |
| Projection head | Random linear projection |
| Optimizer state | Fresh if no checkpoint found |
| Scheduler state | Fresh cosine schedule |
| AMP scaler | Initialized before training |
Italian Training Data Statistics
| Property | Value |
| Language | Italian |
| Dataset | MLS (OpenSLR 94, OPUS) |
| Training split | train |
| Audio files | 59,623 |
| Total duration | ~279 hours |
| Audio format | OPUS |
| Sample rate | Resampled to 16 kHz |
| Validation | None (dev split unavailable locally) |
ICML Standard Practice for Main Experiments and Ablation Studies
| Aspect | Main Experiment | Ablation Experiments |
| Purpose | Establish the best-performing full model | Analyze the contribution of individual components |
| Hyperparameter Search | Allowed and encouraged | Not performed |
| Validation Usage | Hyperparameters selected on a development / validation set | Same hyperparameters as the main experiment |
| Hyperparameter Settings | Tuned to obtain a single optimal configuration | Frozen to the main experiment configuration |
| What Is Modified | Model architecture and loss formulation during tuning | Only one component at a time |
| Typical Modifications | Loss weights, temperatures, learning rates | Remove a loss term, remove a module, or replace a modeling assumption |
| Fairness Criterion | Best achievable performance under validation tuning | Controlled comparison under identical settings |
| Reviewer Expectation | Demonstrates competitiveness | Ensures causal interpretability of improvements |
| Category | Phase 1 (Smallest) | Phase 2 (Extended) |
| Languages | Italian, Portuguese, Polish | Phase 1 + Spanish |
| Total Audio Duration | ~511 hours | ~1,429 hours |
| Segment Count | ~135,000 files | ~363,000 files |
| Estimated Storage (Opus, 16 kHz) | ~15–20 GB | ~45–60 GB |
| Recommended Storage Buffer | ~40–50 GB (2.5×) | ~110–150 GB (2.5×) |
| Audio Format Efficiency | Opus @16 kHz, ~5× smaller than FLAC with near-transparent quality | Same as Phase 1 |
| Segment Length | Mostly 10–20 seconds, optimized for GPU VRAM efficiency | Same as Phase 1 |
| Intended Training Use | Efficient ASR training with reduced I/O and VRAM footprint | Larger-scale ASR training and multilingual extension |
Logged Teacher & Student Model Artifacts
- Place the teacher’s inference within
torch.cuda.amp.autocast(dtype=torch.float16), ensures all calculations are performed under float16, avoiding type conversion issues. Add torch.no_grad() as a context manager to conserve memory (the teacher doesn’t need gradients).
| Log Item | Applies To | Meaning | Why It Exists / What It Tells You |
torch_dtype is deprecated! Use dtype instead! | Both | Warning from Hugging Face API | Indicates an API change; does not affect model correctness or results. Safe to ignore. |
HF_TOKEN does not exist in Colab secrets | Both | Authentication warning | Hugging Face token is optional for public models. No impact on loading Whisper checkpoints. |
config.json | Teacher & Student | Model architecture configuration | Defines model size, layers, hidden dimensions, attention heads, vocab size, etc. |
model.safetensors (3.09 GB) | Teacher (Whisper Large v3) | Full model weights | Contains all frozen parameters of the teacher model (~1.5B parameters). |
model.safetensors (332 MB) | Student (Distil-Whisper Small) | Base student weights | Contains the pretrained student backbone before LoRA injection. |
generation_config.json | Both | Decoding configuration | Stores generation defaults (beam size, length penalties, etc.). Used for inference, not training. |
preprocessor_config.json | Both | Audio preprocessing setup | Defines log-mel extraction, sampling rate, feature normalization. |
tokenizer_config.json | Both | Tokenizer metadata | High-level tokenizer settings (padding, truncation, model type). |
vocab.json | Both | Token vocabulary | Maps tokens to integer IDs. Shared or nearly shared between teacher and student. |
tokenizer.json | Both | Fast tokenizer graph | Serialized tokenizer for efficient runtime tokenization. |
merges.txt | Both | BPE merge rules | Defines subword merges for Byte Pair Encoding. |
normalizer.json | Both | Text normalization rules | Controls lowercasing, punctuation handling, unicode normalization. |
added_tokens.json | Both | Extra special tokens | Language tokens, task tokens, timestamp tokens, etc. |
special_tokens_map.json | Both | Special token mapping | Identifies BOS, EOS, PAD, language tokens, and task markers. |
trainable params: 15,728,640 | Student only | Parameters updated during training | Includes LoRA adapters + projection head. These are the only parameters optimized. |
all params: 181,860,864 | Student only | Total student parameter count | Includes frozen base Whisper weights + LoRA + heads. |
trainable%: 8.6487 | Student only | Fraction of trainable parameters | Shows parameter-efficient learning: <9% of student parameters are updated. |
Core Generative Model Paradigms (Images / Video / Science)
| Model | Proposed by (Year) | Model Type | Core Idea (Essence) |
| Stable Diffusion | Stability AI et al. (2022) | Diffusion Model | Learn to reverse Gaussian noise step-by-step to generate images from text. |
| DALL·E | OpenAI (2021–2023) | Diffusion Model | Text-conditioned diffusion for image synthesis with strong semantic alignment. |
| OpenAI Sora | OpenAI (2024) | Diffusion + World Model | Diffusion in latent spacetime, learning physical and temporal consistency. |
| Meta MovieGen | Meta (2024) | Diffusion Model | High-fidelity video generation via large-scale diffusion with motion priors. |
| AlphaFold3 | DeepMind (2024) | Diffusion + Geometric Modeling | Diffusion over 3D molecular structures (proteins, DNA, ligands). |
| RFDiffusion | Baker Lab (2023) | Diffusion Model | Generate novel protein backbones via structure-space diffusion. |
Gradient Accumulation For Whisper-large-v3
| Aspect | What Happens | Why It Hurts Gradient Accumulation |
| Non-linear compute | Audio → Mel → Encoder with O(T²) attention | Compute does not scale linearly with batch size |
| Heavy padding | Large variance in audio length inside a batch | Short clips still pay for long ones |
| Per-forward overhead | Padding masks, attention layouts, kernel scheduling | Repeated every micro-batch |
| Attention kernels | Depend on actual sequence length | Cannot be reused efficiently |
| GPU scheduling | Kernel launch & layout setup dominate | Overhead > useful compute |
Role of Validation Loss in Multilingual KD Training
| Aspect | Conventional Supervised Training | Our Multilingual KD Setting |
| Primary risk | Data overfitting | Objective overfitting |
| Cause of overfitting | Memorization of training samples | Over-optimization of auxiliary distillation losses |
| Role of validation loss | Detect memorization | Detect misalignment between surrogate losses and token-level accuracy |
| What validation loss measures | Generalization gap | When representation-level alignment no longer improves decoding |
| Mitigation strategy | Early stopping | Stage-wise loss reweighting and auxiliary loss decay |
Backpropagation
| Stage | Operation | Expression | Meaning |
| Forward Pass | Compute layer outputs | \(z^{(l)} = W^{(l)} a^{(l-1)} + b^{(l)}, \quad a^{(l)} = f(z^{(l)})\) | Obtain network predictions |
| Compute Loss | Compute error | \(L = \tfrac{1}{2}|\hat{y} - y|^2\) | Measure output error |
| Backward Pass | Backpropagate from output layer | \(\delta^{(L)} = (\hat{y} - y) \odot f'(z^{(L)})\) | Compute output-layer gradient |
| | Propagate to previous layers | \(\delta^{(l)} = (W^{(l+1)})^T \delta^{(l+1)} \odot f'(z^{(l)})\) | Compute hidden-layer gradients |
| Gradient Computation | Compute parameter gradients | \(\frac{\partial L}{\partial W^{(l)}} = \delta^{(l)} (a^{(l-1)})^T\) | Obtain weight gradients |
| Update | Update parameters | \(W^{(l)} \leftarrow W^{(l)} - \eta \frac{\partial L}{\partial W^{(l)}}\) | Optimize via gradient descent |
Optimal Method as Below with Hash Value
| Problem | Original Complexity | Optimal Complexity | Optimal Method | Further Optimization |
| Check Anagram | O(n) | O(n) | Counter / Hash Map | Cannot Be Improved |
| Dictionary Anagram Lookup | O(M × N log N) | O(M × N) | Hash Value + Character Count Key | Significantly Optimizable |
Hash Map and Graph for Optimization
| Analogy | Hash Map in Data Structures | Dynamic Programming / Graph in Algorithms |
| Essence | Trade space for time — achieve O(1) lookup. | Trade state-graph computation for optimal solution — typically O(N × M). |
| Advantage | Globally optimal method for key lookup. | Globally optimal framework for decision and optimization. |
| Limitation | Only applicable to key–value lookup problems. | Only applicable to decomposable problems with optimal substructure. |
| Conclusion | The most efficient in the lookup domain. | The most general but not universal in the optimization/decision domain. |
Languages
| Dimension | Rust | Go (Golang) | C++ | Python |
Essentially OOP | ✗ (OOP-like, but primarily functional) | ✗ (Has OOP features, but fundamentally procedural and concurrent) | ✓ (Classic, strongly object-oriented) | ✓ (Dynamic, fully object-oriented) |
| Programming Paradigm | Multi-paradigm: Primarily functional + systems, supports OOP traits | Procedural + concurrent, limited OOP | Multi-paradigm: Strongly object-oriented + generic | Multi-paradigm: Object-oriented + scripting |
| Type System | Static, compiled | Static, compiled | Static, compiled | Dynamic, interpreted |
| Memory Management | No GC; uses ownership + borrow checker | Automatic GC | Manual (new/delete) or smart pointers | Automatic GC |
| Concurrency Model | Lock-free, type-safe (“fearless concurrency”) | Goroutines + channels (CSP model) | Multithreading with manual locks | GIL limits true multithreading |
| Performance | Nearly equal to C++ | Close to C++, slightly slower (GC overhead) | Fastest native performance | Slowest (interpreted) |
| Safety | Compile-time memory safety; prevents data races | Memory-safe but not thread-safe | Very fast but error-prone (dangling pointers, overflows) | Safe but slow |
| Learning Curve | Steep (requires ownership understanding) | Easy (simple syntax) | Steep (complex syntax and templates) | Easiest (beginner-friendly) |
| Compile Speed | Slow | Fast | Slow (especially for large projects) | None (interpreted) |
| Ecosystem | Young but growing fast (systems, embedded, backend) | Mature (cloud, DevOps, microservices) | Broadest (systems, games, embedded) | Broadest (AI, data science, web) |
| Applications | System programming, secure backend, embedded, WebAssembly | Cloud-native systems, microservices, networking | OS, game engines, graphics | AI/ML, scripting, automation, data analysis |
| Philosophy | “Zero-cost abstraction” — safety + performance | “Pragmatic simplicity” — simplicity + efficiency | “Total control” — performance + flexibility | “Ease of use” — simplicity + rapid prototyping |
| Key Projects | Firefox, Tokio, AWS Firecracker | Docker, Kubernetes, Terraform | Unreal Engine, Chrome, TensorRT | PyTorch, TensorFlow, YouTube |
C++, Python
| Language | Execution Pipeline | Abstraction Level | Real-World Performance |
| C/C++ | Source code → Compilation → Machine code → Executed directly by the CPU one-step execution | Direct (no virtual layer) | ≈ 100% (baseline) |
| Java | Source code → Bytecode (.class) → JVM → Interpreted / JIT-compiled one extra layer | Virtual machine layer | ⚡ ≈ 70 – 100% of C++, sometimes faster |
| Python | Source code → Interpreter → Dynamic execution multiple layers | Interpreter + dynamic typing | ≈ 1 – 5% of C++ |
C++
- Designed as a systems programming language, “Generate code that maps directly to hardware”
C++/CUDA code (.cu)
↓ nvcc compile
PTX / SASS GPU machine code
↓
GPU executes the kernel directly
Python
- Designed as a high-level dynamic scripting language, “Maximize developer productivity and readability, not performance”
Python code (.py)
↓
Calls into C/C++ library (PyTorch, TensorFlow, NumPy, CuPy…)
↓
C/C++ implementation launches CUDA kernels
↓
GPU executes the kernel
DNS
| IP Address | Service / Network | Description |
| 129.132.98.12 | ETH Zurich Primary DNS | Main campus DNS; default resolver used by EULER and VPN connections. |
| 129.132.250.2 | ETH Zurich Secondary DNS | Backup DNS paired with the primary resolver above. |
| 129.132.250.10 | SIS / Leonhard / LeoMed DNS | Internal DNS for Leonhard, LeoMed, and SIS Research IT environments. |
| 129.132.250.11 | SIS / Backup DNS | High-availability (HA) redundant DNS for research and secure clusters. |
Unix vs Linux - Concise Comparison
| Aspect | Unix (1969) | Linux (1991) |
| Creator | AT&T Bell Labs (Ken Thompson, Dennis Ritchie) | Linus Torvalds |
| Motivation | Replace the bloated Multics system with a simple, reliable operating system | Provide a free, Unix-compatible system that runs on inexpensive hardware |
| Cost | Expensive, proprietary | Free and open-source |
| License | Vendor-specific, closed-source | GNU GPL (open-source) |
| Status Today | Legacy and declining (e.g., Solaris, AIX, HP-UX) | Dominant platform (over 90% of servers, all top supercomputers) |
| Core Philosophy | Modularity: “Do one thing, and do it well” | Democratization of Unix through open collaboration |
- Unix laid the foundation in 1969 → Linux made Unix free and ubiquitous in 1991 → EOF enables clean multi-line command input in Bash.
Latent Space Structure
| Space | Core Definition | Difference from Others | Application Domains |
Hilbert Space | A complete inner product space where lengths, angles, and projections are well-defined | Serves as the foundational “perfect” geometric space; all others are generalizations or relaxations | Quantum mechanics, signal processing, optimization, machine learning |
| Banach Space | A complete normed vector space, not necessarily with an inner product | Has length but no angles | Non-Euclidean optimization, functional analysis |
| Riemannian Manifold | Each point has a local inner-product space (tangent space) | Locally Hilbert, globally curved | General relativity, geometric deep learning |
| Symplectic Space | Equipped with an area-preserving bilinear form | No distance, only conserved quantities | Classical mechanics, Hamiltonian systems |
| Topological Space | Defined only by neighborhood relationships, no metric required | No notion of length or angle | Generalized geometry, continuity, homotopy theory |
| Metric Space | A set with a defined distance function d(x, y) | Hilbert space is a special case | Clustering, manifold learning, distance-metric learning |
| Probability Space | A measurable space (Ω, F, P) defining random events | Describes the geometry of events | Probability theory, information geometry, Bayesian inference |
| Information Manifold | A Riemannian manifold on probability distributions | Uses Fisher information metric | Statistical inference, information geometry, variational inference |
| Kähler / Complex Space | Complex structure + symmetric geometry + metric | Conformal generalization of Hilbert space | Quantum geometry, string theory, complex optimization |
Algorithms
├── I. Data Structures
│ ├── Stack, Queue, <HashMap>, LinkedList
│
├── II. Algorithmic Patterns
│ ├── Two Pointers
│ ├── Sliding Window
│ ├── Prefix Sum
│ ├── Monotonic Stack / Queue
│ ├── Binary Search Patterns
│
├── III. Complex Algorithms
│ ├── <Dynamic Programming (DP)>
│ ├── <Graph Theory (DFS/BFS/Dijkstra)>
│ ├── Recursion / Backtracking
│ ├── Greedy Algorithms
│ ├── Divide & Conquer
│
└── IV. Problem Integration
├── Hard composite problems
├── Algorithm design questions
Diffusion, Stable Diffusion, Rectified Flow
| Dimension | Vanilla Diffusion Model (DDPM / DDIM) | Stable Diffusion (Latent Diffusion Model, LDM) | Rectified Flow (Flow Matching) |
| Start Distribution | Starts from pure Gaussian noise N(0, I) | Starts from latent-space noise (compressed through an encoder) | Starts from any distribution point (usually N(0, I), but customizable) |
| Generative Process | Multi-step denoising: reverses the noise diffusion process (xₜ₋₁ = fθ(xₜ, t)) | Multi-step denoising in latent space (computationally cheaper) (zₜ₋₁ = fθ(zₜ, t)) | Continuous one-step flow: learns an ODE (dxₜ/dt = vθ(xₜ, t)) |
| Mathematical Formulation | Discrete Markov chain (reverse SDE) | Discrete SDE in latent space | Continuous ODE or flow field |
| Computational Complexity | Multi-step sampling (20–1000 steps) | Multi-step but faster in latent space (20–50 steps) | Single continuous integration step |
| Advantages | High generation quality; theoretically grounded | High resolution, lightweight, and controllable (supports text prompts) | Fast convergence, continuous generation, minimal mode collapse |
| Limitations | Slow sampling; many denoising steps required | Strong dependence on encoder design and latent structure | Sensitive training stability; harder conditional control |
| Representative Papers / Applications | DDPM (Ho et al., 2020); DDIM (Song et al., 2021) | LDM / Stable Diffusion (Rombach et al., CVPR 2022) | Flow Matching / Rectified Flow (Liu et al., ICLR 2023) |
Optimization
| Component / Technique | Description | Implementation |
| Optimizer | Gradient-based weight updates with decoupled weight decay to improve stability on large models. | AdamW optimizer with lr=2.6e-4 and default β=(0.9, 0.999); stable for transformer-like models. |
| Learning-Rate Schedule | Smooth cosine decay to avoid abrupt gradient shocks after warm-up. | get_cosine_schedule_with_warmup(opt, 1000, 10000) — warm-up = 1 k steps, total = 10 k steps. |
| Warm-Up Phase | Gradually increases learning rate and KL weight to prevent early divergence in distillation. | Linear warm-up for both learning rate and λₖₗ (0 → 0.020584 during first 1000 steps). |
| Mixed-Precision Training | Uses half precision (torch.amp.autocast) to reduce GPU memory and improve throughput. | Forward/backward passes wrapped in autocast, scaled by GradScaler() for numerical stability. |
| Gradient Clipping | Prevents exploding gradients in long sequences. | torch.nn.utils.clip_grad_norm_(params, 1.0) each iteration. |
| Loss Function (Multi-Objective) | Balances semantic accuracy, distribution matching, and geometric alignment. | Total loss: L = LCE + λₖₗ · LKL + λGeo · LGeo, with λGeo = 0.969909 constant. |
| CE Loss | Supervised label alignment ensuring correct transcription semantics. | Cross-entropy between student predictions and true tokens. |
| KL Divergence | Soft-target distillation to transfer probability distributions from teacher logits. | F.kl_div(log_softmax(student/T), softmax(teacher/T)) · T², T = 2.0. |
| Riemannian Geodesic Loss | Aligns feature geometry on curved manifold instead of flat Euclidean MSE. | Geodesic distance = acos(cos_sim) between normalized hidden states. |
| Model Architecture (Student) | Lightweight CNN + Transformer hybrid for speech sequence modeling. | Two 1-D Conv layers → 6 Transformer encoder blocks → linear output head. |
| Teacher Model | Provides target logits and hidden features for distillation. | Frozen Whisper-large-v2 (FP16) encoder-decoder model. |
distil_run_cell2.7.2/
│
├── tb/ ← TensorBoard log files
│ ├── events.out.tfevents...
│
├── adapter_final/ ← Final trained student model
│ └── student_model.pt
│
├── checkpoint.pt ← Intermediate checkpoint (used if training was interrupted)
├── training_history.json ← Recorded training and validation loss curves
├── best_params.json ← Best hyperparameter record (e.g., kl_weight, geo_weight)
└── training_config.json ← Training configuration and setup details
Structure
Machine Learning Fundamentals
│
├── Data → Representation → Optimization → Generalization
│ ├─ Focus: Data quality, bias mitigation, and representation learning
│ ├─ Link to Gemini: multimodal data fusion (text, audio, vision, code)
│ └─ Goal: Learn unified latent spaces that enable reasoning across modalities
│
├── Deep Learning (CNN / RNN / Transformer)
│ ├─ Forward & backward propagation as differentiable computation graphs
│ ├─ Initialization, normalization, regularization → stability & convergence
│ ├─ Loss design + learning rate scheduling → control of optimization dynamics
│ └─ Transformer family as universal sequence learners (foundation for Gemini)
│
├── Optimization & Geometry
│ ├─ Gradient-based optimization viewed as navigating the loss landscape
│ ├─ Flat vs. sharp minima → generalization and robustness trade-offs
│ ├─ Riemannian geometry in embedding space → alignment on curved manifolds
│ └─ Connection: Gemini’s embedding consistency and representation curvature
│
├── Model Compression & Distillation
│ ├─ Knowledge transfer from large to small models (teacher → student)
│ ├─ Soft vs. hard labels → probabilistic vs. symbolic supervision
│ ├─ LoRA / Adapter-based fine-tuning → parameter-efficient adaptation
│ ├─ Trade-offs: accuracy ↔ latency ↔ memory footprint ↔ energy efficiency
│ └─ Relevance: LearnLM and Gemini use adapter-tuned submodels for learning tasks
│
└── ML Engineering & Responsible AI
├─ Data pipelines, reproducibility, evaluation, and continuous integration
├─ Monitoring, checkpointing, scalable deployment on distributed accelerators
├─ Safety alignment and interpretability — understanding model decisions
├─ Evaluation beyond accuracy: robustness, fairness, value alignment
└─ Ethical ML engineering: accountability and transparency in large systems
Time
| Big-O | Name | Typical Example |
| O(1) | Constant time | Accessing array element |
| O(log n) | Logarithmic time | Binary search |
| O(n) | Linear time | Single loop through array |
| O(n log n) | Linearithmic time | Merge sort, Quick sort |
| O(n²) | Quadratic time | Nested loops, Bubble sort |
| O(n³) | Cubic time | Triple nested loops |
| O(2ⁿ) | Exponential time | Subset / permutation generation |
| O(n!) | Factorial time | Traveling Salesman, N-Queens |
| O(bᵈ) | Branching search | DFS in state tree with branching b and depth d |
O(n): O(n log n): O(n²):
loop → → → divide → sort → merge double loop → compare all
(one pass) (log layers × n work) (each pair compared)
linear scan merge / quick sort bubble / selection sort
Space
| Big-O | Name | Typical Example |
| O(1) | Constant space | In-place swap, variable assignment |
| O(log n) | Logarithmic space | Recursive binary search |
| O(n) | Linear space | Storing array, dynamic programming 1-D |
| O(n²) | Quadratic space | 2-D matrix, Floyd-Warshall DP |
| O(n³) | Cubic space | 3-D DP table |
| O(2ⁿ) | Exponential space | Memoization of all subsets |
Data Loader
| Stage | Code Section | Padding Applied | Explanation |
| ① Dataset structure check | os.walk() file scan | No | Only scans file names, counts, and sizes. |
| ② Load audio–text pairs | pairs = load_audio_text_pairs(DATA_DIR) | No | Generates file paths, no tensor involved. |
| ③ Build Dataset | dataset = LibriSpeechLocalDataset(pairs, processor) | Not yet | Each sample is returned separately, no unified length. |
| ④ Build DataLoader | train_loader = DataLoader(...) | Yes (here) | Padding is applied when combining samples into a batch. |
| ⑤ Train model | for step, batch in enumerate(train_loader): | Already padded | Batch tensors have equal dimensions for training. |
Protocol and Ports
[You: MacBook] ←→ [Encrypted Tunnel (AES)] ←→ [Mac Studio Server]
↕ ↕
ssh user@ip_address sshd (daemon listening on port 22)
| Protocol | Port | Purpose |
| HTTP | 80 | Web traffic |
| HTTPS | 443 | Secure web traffic |
| FTP | 21 | File transfer |
| SSH | 22 | Secure remote shell |
| Function | Command Example | Description |
Remote Login | ssh user@192.xxx.x.xx | Open a command-line session on a remote computer |
File Transfer | scp file.txt user@host:/path/ | Securely copy a file to a remote machine |
Port Forwarding | ssh -L 8080:localhost:80 user@host | Map a remote port to a local port through an encrypted tunnel |
| Passwordless Login | Public key authentication (~/.ssh/id_rsa.pub) | Automatically authenticate using key pairs |
| Automation Control | Use SSH to execute commands or sync data in bulk | Common in DevOps or HPC environments |
Optimizers
| Era | Optimizer | Year | Core Innovation | Key Equation / Concept | Limitation Solved | Remarks |
| Classical GD | Gradient Descent (GD) | 1951 | Update weights along the negative gradient direction | \(w_{t+1} = w_t - \eta \nabla L(w_t)\) | None (too simple) | Foundation of all optimizers |
| | Stochastic Gradient Descent (SGD) | 1983 | Uses random mini-batches to improve efficiency | \(\nabla L(w_t) \approx \frac{1}{\lvert B \rvert} \sum_{i \in B} \nabla L_i(w_t)\) | High variance and slow convergence | Enables online / large-scale learning |
| Momentum Era | SGD + Momentum | 1989 | Adds velocity term to accumulate past gradients | \(v_t = \beta v_{t-1} + (1-\beta)\nabla L(w_t), \quad w_{t+1} = w_t - \eta v_t\) | Oscillations in narrow valleys | Faster convergence, physics-inspired |
| | Nesterov Accelerated Gradient (NAG) | 1991 | Looks ahead using gradient of estimated future position | \(v_t = \beta v_{t-1} + (1-\beta)\nabla L(w_t - \eta \beta v_{t-1})\) | Overshooting in Momentum | Smoother convergence and stability |
| Adaptive Learning | Adagrad | 2011 | Per-parameter adaptive learning rate | \(G_t = \sum_{\tau=1}^{t} g_\tau^2, \quad \eta_{t,i} = \frac{\eta}{\sqrt{G_{t,i}}+\epsilon}\) | Manual learning rate tuning | Excellent for sparse features (NLP) |
| | RMSProp | 2012 | Exponentially weighted moving average of squared gradients | \(v_t = \rho v_{t-1} + (1-\rho)g_t^2, \quad w_{t+1} = w_t - \frac{\eta}{\sqrt{v_t+\epsilon}}g_t\) | Adagrad’s decaying rate problem | Stable for non-stationary objectives |
| Modern Standard | Adam | 2014 | Combines Momentum and RMSProp | \(m_t = \beta_1 m_{t-1} + (1-\beta_1)g_t, \quad v_t = \beta_2 v_{t-1} + (1-\beta_2)g_t^2\) \(\hat{m}_t = \frac{m_t}{1-\beta_1^t}, \quad \hat{v}_t = \frac{v_t}{1-\beta_2^t}, \quad w_{t+1} = w_t - \eta \frac{\hat{m}_t}{\sqrt{\hat{v}_t}+\epsilon}\) | Gradient noise and curvature imbalance | Default optimizer for most deep networks |
| | AdamW | 2017 | Decouples weight decay from gradient update | \(w_{t+1} = w_t(1-\eta\lambda) - \eta \frac{m_t}{\sqrt{v_t}+\epsilon}\) | L2 regularization bias in Adam | Default for Transformer / LLM training |
| Geometry-Aware & Large Batch | LARS (Layer-wise Adaptive Rate Scaling) | 2018 | Layer-wise adaptive learning rate | \(\eta_l = \eta \frac{|w_l|}{|g_l|+\epsilon}\) | Scale mismatch in large-batch training | Used in ResNet / ImageNet large-batch setups |
| | LAMB (Layer-wise Adaptive Moments) | 2019 | Extends LARS with Adam-style moments | \(r_t = \frac{|w_t|}{|\hat{m}_t / (\sqrt{\hat{v}_t}+\epsilon)|}, \quad w_{t+1}=w_t - \eta r_t \frac{\hat{m}_t}{\sqrt{\hat{v}_t}+\epsilon}\) | Poor scaling of Adam for huge batches | Core optimizer for BERT, GPT |
| Variance Rectification & Belief Models | RAdam | 2019 | Rectifies variance of adaptive learning rate | \(\eta_t = \eta \frac{\sqrt{(1-\beta_2^t)/(1-\beta_2)}}{\sqrt{v_t}+\epsilon}\) | Instability in early training | More robust warm-up-free Adam |
| | AdaBelief | 2020 | Tracks belief in gradient direction | \(v_t = \beta_2 v_{t-1} + (1-\beta_2)(g_t - m_t)^2\) | Gradient over-smoothing | Better generalization for small datasets |
| Second-Order & Natural Gradient | K-FAC (Kronecker-Factored Approximate Curvature) | 2015–2023 | Approximates curvature via blockwise Kronecker products | \(F^{-1} \approx A^{-1} \otimes B^{-1}, \quad w_{t+1} = w_t - \eta F^{-1}\nabla L\) | Ignores curvature in SGD/Adam | Faster convergence, heavy memory use |
| | Shampoo | 2021 | Matrix preconditioning per layer | \(G_t = \sum_{\tau=1}^{t} g_\tau g_\tau^\top, \quad W_{t+1}=W_t - \eta G_t^{-1/2}\nabla L\) | Slow convergence on ill-conditioned loss | Improves conditioning for large models |
| Modern LLM Optimizers | Lion | 2023 | Momentum with sign-based updates | \(w_{t+1} = w_t - \eta \, \text{sign}(\beta_1 m_t + (1-\beta_1)g_t)\) | Over-adaptation of Adam | Efficient and strong generalization for LLMs |
| | Sophia | 2023 | Second-order curvature-aware optimizer | \(w_{t+1} = w_t - \eta \frac{g_t}{\sqrt{h_t+\epsilon}}, \quad h_t \approx \text{diag}(H_t)\) | Slow convergence in large-scale Adam | State-of-the-art for Transformer training |
Riemannian Projector, Geodesic Loss
class RiemannianProjector(nn.Module):
def __init__(self, in_dim=768, out_dim=1280):
...
def forward(self, x):
x = self.map(x)
return F.normalize(x, dim=-1)
cos_sim = (x*y).sum(-1)
loss = acos(cos_sim)
Teacher (Whisper-large-v2, frozen)
│
▼
Student (<Structure-free> Student from the teacher + LoRA adapters)
│
├── CE loss (labels supervision)
│ ↑
│ └── Hard labels = ground truth text
│ (e.g. “Hello world” from dataset)
│
├── KL loss (soft logits distillation)
│ ↑
│ └── Soft labels = teacher’s predicted probabilities
│ (e.g. P(“hello”)=0.62, P(“hey”)=0.31, P(“halo”)=0.07)
│
└── Geo loss (Riemannian alignment)
↑
└── Aligns latent embeddings on a curved manifold
(ensures student follows teacher’s geometry)
↓
Optimizer (AdamW + Cosine LR)
↓
LoRA Adapter Checkpoint
↓
Evaluation (WER / RTF / Memory)
s_hid = student_proj(s_out.encoder_last_hidden_state)
t_hid = normalize(t_out.encoder_last_hidden_state)
geo = geodesic_distance_on_sphere(s_hid, t_hid)
TAID
Initial training (step=0): λ=0.1 intermediate = 0.9 * student_probs + 0.1 * teacher_probs
→ Mainly learn the student’s own distribution
Mid-training (step=400): λ≈0.5 intermediate = 0.5 * student_probs + 0.5 * teacher_probs
→ Balanced learning
Late training (step=800): λ=0.9 intermediate = 0.1 * student_probs + 0.9 * teacher_probs
→ Mainly learn the teacher’s distribution
Background Knowledge
RL On Diffusion
I. Base Diffusion Backbone (Generative Prior)
Input (x₀ = real data sample: image, trajectory, audio, 3D scene)
↓
Forward Diffusion Process (adds Gaussian noise)
↓
x₁ ← √α₁·x₀ + √(1−α₁)·ε₁
x₂ ← √α₂·x₁ + √(1−α₂)·ε₂
⋮
x_T ≈ pure Gaussian noise N(0, I)
↓
Reverse Denoising Process (parameterized by neural network ε_θ)
↓
x_{t−1} = (x_t − √(1−α_t)·ε_θ(x_t, t, cond)) / √α_t + η·σ_t
↓
UNet / Transformer backbone → learns to reconstruct x₀
II. Policy Representation via Diffusion
Environment State s_t
↓
Noise z_t ~ N(0, I)
↓
Diffusion Policy Network ε_θ(s_t, z_t, t)
↓
Sample Action a_t = Denoise(z_t | s_t)
↓
Execute Action in Environment → Receive Reward r_t
↓
Collect Trajectory τ = {s_t, a_t, r_t}

IV. Reward-Guided Diffusion Training (Diffusion Policy Optimization)
For each episode:
1. Sample noise x_T ~ N(0, I)
2. Run reverse diffusion (ε_θ) conditioned on state s_t
3. Generate predicted action trajectory x₀
4. Execute in environment → collect reward R
5. Compute loss:
L_total = L_diffusion + λ·L_RL
L_RL = − E[R(τ)]
6. Backpropagate through ε_θ network
Diffusion Policy, Decision Diffuser
Random Noise in Action Space
↓
Diffusion or Flow Process
↓
Denoising Steps / Continuous Flow
↓
Policy Network predicts εθ(x_t,t)
↓
Clean Action Sequence (Optimal Trajectory)
↓
Execute in Environment (Robotics / Control)
| Function | Formula | Derivative | Core Idea | Usage / Notes |
| Sigmoid | \(f(x) = \frac{1}{1 + e^{-x}}\) | \(f'(x) = f(x)\,[1 - f(x)]\) | Smooth bounded mapping (0, 1) | Common in probabilistic outputs |
| Tanh | \(f(x) = \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}\) | \(f'(x) = 1 - f(x)^2\) | Zero-centered output | Improves symmetry over Sigmoid |
| ReLU | \(f(x) = \max(0,\,x)\) | \(f'(x)=\begin{cases}1,&x>0\\0,&x\le0\end{cases}\) | Sparse and efficient | Fast convergence, stable training |
| Leaky ReLU | \(f(x)=\max(\alpha x,\,x)\) | piecewise constant | Avoids dead neurons | Small negative slope for x < 0 |
| Swish / SiLU | \(f(x)=x\,\sigma(x),\ \sigma(x)=\frac{1}{1+e^{-x}}\) | \(f'(x)=\sigma(x)+x\,\sigma(x)[1-\sigma(x)]\) | Smooth, self-gated ReLU | Used in Google EfficientNet |
| Mish | \(f(x)=x\,\tanh(\ln(1+e^x))\) | smooth | Non-monotonic, better gradient flow | Used in YOLOv4, ResNet variants |
| GELU | \(f(x)=x\,\Phi(x),\ \Phi(x)\text{: Gaussian CDF}\) | smooth | Probabilistic gating | Default in Transformers (BERT, GPT) |
| JumpReLU (DeepMind) | \(f(x)=\max(0,\,x-j),\ j\text{ learned}\) | piecewise constant | Learnable sparsity threshold | Used in Sparse Autoencoders for interpretability |
| Softmax | \(f_i(x)=\frac{e^{x_i}}{\sum_j e^{x_j}}\) | — | Converts logits → probabilities | Standard output for classification |
Learning Rates
| Trend | Description | Representative Systems |
| Cosine + Warmup → Standard Default | Most stable across architectures. | ViT, GPT-J, Whisper, Stable Diffusion |
| Adaptive + Restart Hybrids | Combine SGDR + ReduceLROnPlateau. | DeepSpeed, Megatron-LM, PaLM 2 |
| Optimizer-Integrated Scheduling | Scheduler coupled with optimizer (AdamW, LAMB). | GPT-4, Gemini 1.5, Claude 3 |
| Noisy / Stochastic Schedules | Inject noise to encourage flat minima. | Google Brain NAS, RL-based training |
| Dynamic Data-Aware LR Control | LR adapted by validation loss or gradient norm. | Reinforcement fine-tuning (RLHF, PPO) |
Scaling Law
| Year | Model | Number of Layers | Parameter Count | FLOPs (per inference) | Activations (per forward pass) | Typical Memory Footprint |
| 1998 | LeNet | 5 | ~0.1 M | ~0.001 GFLOPs | < 1 MB | < 10 MB |
| 2012 | AlexNet | 8 | 60 M | ~1.5 GFLOPs | ~100 MB | ~1 GB |
| 2015 | VGG-16 | 16 | 138 M | ~15 GFLOPs | ~200 MB | ~2–4 GB |
| 2016 | ResNet-152 | 152 | 60 M | ~11 GFLOPs | ~250 MB | ~4–6 GB |
| 2018 | BERT-Large | 24 | 340 M | ~180 GFLOPs | ~1 GB | ~10–12 GB |
| 2020 | GPT-3 | 96 | 175 B | ~3.1 × 10¹² FLOPs | ~20 GB | ~350 GB (weights) / > 1 TB (training) |
| 2024 | GPT-4 / Gemini 1.5 / Claude 3 | ~120 – 200 | > 1 T (trillion) | ~10¹³ – 10¹⁴ FLOPs | > 50 GB (activations) | Multiple TB (large-scale training) |
Generalization and Regularization
Underfitting: Overfitting: Good Embedding:
• • • • • ●●● ○○○ ▲▲▲ ● ● ○ ○ ▲ ▲
○ ○ ○ ○ ○ (tight) (tight) (clear but smooth)
▲ ▲ ▲ ▲ ▲ val points outside val & train overlap
| Principle | Intuition |
| Regularization = adding controlled noise or constraints to prevent memorization. | Introduces noise or limits (e.g., dropout, weight decay, data augmentation) so the model learns general patterns instead of memorizing the training set.
|
| Overfitting = perfect fit on training data, poor generalization. | The model minimizes training loss too well, capturing noise instead of true structure — leads to poor performance on unseen data.
|
| Goal = flatter minima + smoother decision boundaries. | Seek regions in the loss landscape where small parameter changes do not greatly affect loss — resulting in more stable, generalizable models.
|
CNN
[Input D×E (image or signal)]
│
▼
[Convolution U×V (kernel/filter)]
│ learns local spatial patterns
│ parameters ≪ fully-connected layers
▼
[Zero-Padding / Stride Control]
│
├─ Padding → keeps size (same)
└─ Stride → downsamples (D−U)/S+1
▼
[Feature Map K×M (activation before nonlinearity)]
│
▼
[Activation g(a) → ReLU / Sigmoid / Tanh]
│
▼
[Pooling R×R window (Avg / Max / Global)]
│
├─ replaces stride for down-sampling
├─ reduces spatial size, increases receptive field
└─ enhances translation invariance
▼
[Stacked Conv + Pooling Layers]
│
├─ small kernels (3×3) + pooling ⇒ large receptive field
├─ more layers > larger kernels (prefer depth)
└─ weights grow linearly w/ layers
▼
[Flatten or Global Pooling]
│
├─ flatten: A ∈ ℝ^{Q×K×M} → a ∈ ℝ^{Q·K·M}
└─ global pooling: spatial avg → a ∈ ℝ^{Q}
▼
[Fully-Connected Layer + Loss]
│
├─ Regression → J_L2
├─ Binary → J_BCE
└─ Categorical → Softmax + J_CCE
▼
[Output Prediction y / Class Probabilities]
Forward Pass
Input (32×32×3)
↓
Conv (3×3 kernel, 16 filters)
↓
ReLU activation
↓
Max Pooling (2×2)
↓
Conv (3×3 kernel, 32 filters)
↓
ReLU
↓
Global Avg Pooling
↓
Flatten → Dense (Fully-connected)
↓
Softmax → [Cat, Dog, Car, …]
Optimization for Training
| Stage | Method | Purpose / Effect |
| Initialization Stage | Xavier / He initialization | Avoid falling into poor regions at the start |
| Early Exploration Stage | Large learning rate + Momentum | Maintain global exploration ability |
| Mid Convergence Stage | Adam / RMSProp + Cosine Annealing | Ensure smooth descent and curvature adaptation |
| Late Fine-tuning Stage | SAM / Entropy-SGD / Weight Decay | Locate flat minima and enhance generalization |
| During Training | Mini-batch noise + Dropout | Prevent getting stuck at saddle points |
| Architectural Level | Residual connections / Normalization layers | Improve gradient flow and smooth the optimization landscape |
Normalization and Regularization in different Model Structures
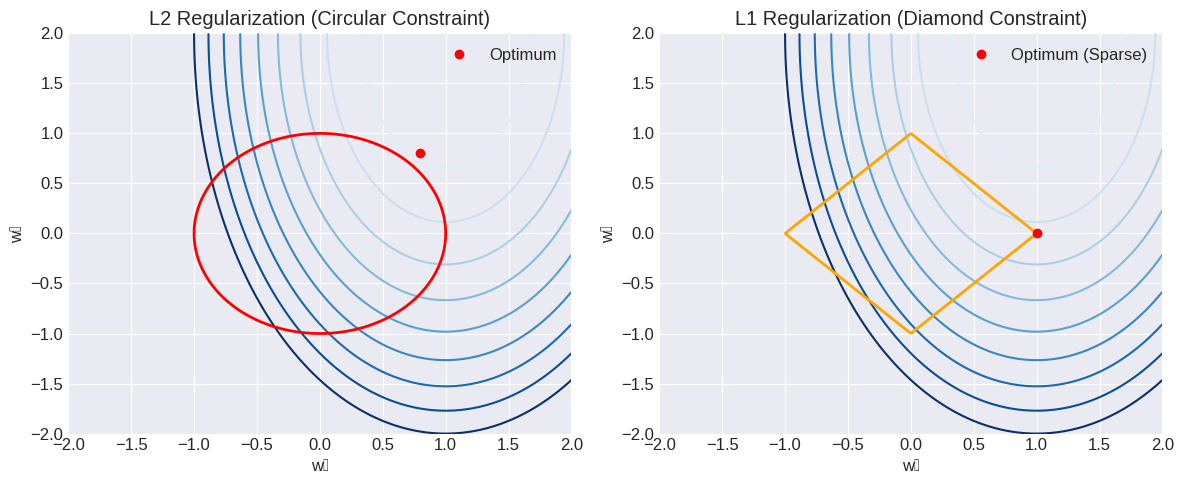
| Item | L1 Regularization | L2 Regularization |
| Shape | Diamond-shaped constraint | Circular constraint |
| Optimum Point | Usually lies on the coordinate axes (sparse solution) | Usually lies on the circle (continuous shrinkage) |
| Result | Some weights are “cut” to exactly 0 | All weights are smoothly reduced but remain non-zero |
| Model Example | Normalization | Regularization | Essence & How It Works |
| CNN (e.g., ResNet) | Batch Normalization — normalizes activations within a mini-batch to stabilize gradients and speed up convergence. | Weight Decay + Dropout — penalizes large weights and randomly drops neurons to reduce overfitting. | Normalization equalizes feature scales during training, while Regularization constrains model capacity to improve generalization. |
| Transformer / LLM | Layer Normalization — normalizes hidden states across features to maintain stable activations in deep attention layers. | Attention Dropout + L2 Regularization — randomly masks attention links and adds weight penalties to prevent overfitting. | Normalization stabilizes internal representations; regularization prevents memorization of training data. |
| MLP | Input Standardization — rescales each input feature to zero mean and unit variance. | L2 Regularization (Ridge) — discourages large parameter magnitudes for smoother mappings. | Normalization improves numerical stability; regularization enforces simpler models with better generalization. |
Optimized Decoding
Classical Decoding (Without KV Cache) Optimized Decoding (With KV Cache)
┌───────────────┐ ┌────────────────────────┐
│ Decoder │ │ Decoder + KV Cache │
│ (Self-Attn) │ │ (Self-Attn + Storage) │
└───────┬───────┘ └──────────┬─────────────┘
│ │
▼ ▼
┌───────────────┐ ┌─────────────────────────┐
│ Recompute all │ O(n²) per step │ Reuse stored K/V │
│ past tokens │ -----------------------------> │ Only new Q calculated │
│ at every step │ │ O(n) per step │
└───────────────┘ └─────────────────────────┘
│ │
▼ ▼
┌─────────┐ ┌───────────────┐
│ Latency │ │ Low Latency │
│ High │ │ On-Device OK │
└─────────┘ └───────────────┘
- Redundant computation - No recomputation
- High memory bandwidth - Lower memory & power
- Slow inference - Faster inference
Training Loop
↓
[ Forward pass ]
↓
[ Compute loss ]
↓
[ Backward pass: compute gradients ]
↓
[ **Gradient Clipping** ] ←— `clip_grad_norm_(model.params, max_norm)`
↓
[ **AdamW Update** ] ←— `optimizer = AdamW(lr=…, weight_decay=…)`
↓
[ Zero Gradients ] ←— `optimizer.zero_grad()`
↓
[ **Cosine LR Annealing** ] ←— `scheduler = CosineAnnealingLR(optimizer, T_max, eta_min)`
↓
[ Next batch ]
Single card peak ~ 13–15 GB VRAM -> Start your Experiment with FP16 + AMP
Whisper large-v3 has the same architecture as the previous large and large-v2 models, except for the following minor differences:
- The spectrogram input uses 128 Mel frequency bins instead of 80
- A new language token for Cantonese
- Each token output by
Attention carries global context information, while FFN applies "fine-tuning" or "feature combination" to each token to improve the feature quality at each position
Transformer Assembly Line
═══════════════════════════════════════════════════════
Raw Donuts → Community Check → Solo Decoration → Finished Donuts
(Input) (Attention) (FFN) (Output)
↓ ↓ ↓ ↓
┌─────────┐ ┌──────────────┐ ┌──────────────┐ ┌─────────┐
│ Plain │→ │ Community │→ │ Solo │ → │Gourmet │
│ Donuts │ │ Analysis │ │ Decoration │ │Donuts │
└─────────┘ └──────────────┘ └──────────────┘ └─────────┘
↓ ↓ ↓ ↓
X₀ X₁ = Attention X₂ = FFN Output
1. X₁ᵢ = Σⱼ αᵢⱼ × V_j (Global Linear)
2. X₂ᵢ = W₂·ReLU(W₁·X₁ᵢ + b₁) + b₂ (Local Nonlinear)
Attention: Convex combination → Stays within input space
FFN: Nonlinear transformation → Can transcend input space
Activation Function Characteristics Comparison
═════════════════════════════════════════════════
┌──────────┬────────────┬───────────────┬──────────────┬─────────────┐
│Function │ Smoothness │ Computational │ Gradient │ Performance │
│ │ │ Complexity │ Properties │ │
├──────────┼────────────┼───────────────┼──────────────┼─────────────┤
│ ReLU │ Non-smooth │ Minimal │ Sparse │ Baseline │
│ GELU │ Smooth │ Moderate │ Dense │ Better │
│ SwiGLU │ Smooth │ High │ Gated │ Best │
│ Mish │ Very Smooth│ High │ Adaptive │ Very Good │
│ Swish │ Smooth │ Moderate │ Self-gated │ Good │
│ ELU │ Smooth │ Moderate │ Negative-safe│ Good │
└──────────┴────────────┴───────────────┴──────────────┴─────────────┘
Input Features From Whisper
┌───────────────────────────────┐
│ Original Domain │
│ - Pixels (Images) │
│ - Samples (Audio, Signals) │
│ - Tokens (Text) │
└───────────────────────────────┘
│
▼ Fourier Transform
┌───────────────────────────────┐
│ Frequency Domain │
│ - Low frequencies → smooth │
│ - High frequencies → edges │
│ - Harmonics → fine details │
└───────────────────────────────┘
│
┌──────────────┼────────────────────┐
▼ ▼ ▼
┌───────────┐ ┌────────────┐ ┌─────────────┐
│ CNNs │ │ Transformers│ │ Speech/Image│
└───────────┘ └────────────┘ └─────────────┘
- Edges = HF - Sinusoidal pos. - STFT / spectrogram
- Smooth = LF encoding - Highlight textures
- Convolutions (frequency basis) - Recognize phonemes
simplified - Detect fine image details
in frequency
space
Teacher (Whisper-large-v2) Student
───────────────────────────── ──────────────────────────────────────────────────
Audio Input Audio Input
1 × T samples 1 × T samples
│ │
▼ ▼
Whisper Encoder Whisper Encoder
1280-d hidden, T~1500 frames 768-d hidden, T~499 frames
(32 layers, FROZEN) (12 layers, FROZEN)
│ │
│ │
├─────── Hidden States ──────────────────────── ├─── Projection Layer ───┐
│ (B,1500,1280) │ (768→1280) │
│ │ │
▼ ▼ ▼
Whisper Decoder Whisper Decoder Aligned Hidden
(32 layers, FROZEN) (4 layers +/ LoRA) (B,1500,1280)
│ │ │
│ │ │
▼ ▼ │
Teacher Logits ────── Soft Targets ─────────▶ Student Logits │
(B,seq,vocab) (KL Loss) (B,seq,vocab) │
│ T=temperature │ │
│ │ │
│ ▼ │
│ Hard Labels ◀── Ground Truth │
│ (CTC Loss) │
│ │ │
│ │ │
│ ▼ │
│ Student Loss ◀─── MSE Loss ──────┘
│ │ (Hidden Align)
│ │
▼ ▼
No parameter updates (LoRA) + Projection parameters
(Inference only) ONLY these are trained
Why T≈499
- Whisper feature extractor
- The original audio (30 s) generates about 3000 frames of 80-dimensional log-Mel features at a granularity of 10 ms per frame
- Whisper first divides the original mono audio (30 seconds, 16 kHz) into several short segments
- Generate an 80-dimensional log-Mel feature every 10 ms
- 30 s / 0.01 s = 3000 frames
- These 3000 frames are still very dense. If Transformer processes them directly, the computational workload and memory requirements will be too high
- Before being fed into the Transformer encoder, these 3000 frames are first downsampled through a convolutional layer (stride=2), and then continuously merged or downsampled in the multi-layer Transformer block
- The final output length is about 3000 / 2 / 3 = 500 frames (actually 499 frames)
30 s audio
⇓ (extract 80-dim log-Mel every 10 ms)
3000 frames
⇓ (convolutional layer with stride=2)
1500 frames
⇓ (further down-sampling/merging inside the Transformer encoder ≈×3)
⇓ (Pooling or Conv1d: kernel_size=3, stride=3)
≈500 frames (actually 499 frames)
- Audio Signal Characteristics - Redundancy -> why can be compressed to T~499 frames
1. Audio frame rate is typically high
sample_rate = 16000 # 16 kHz sampling rate
frame_rate = 100 # 100 frames per second
frame_duration = 10 # 10 ms per frame
2. 30 seconds of audio
total_frames = 30 * frame_rate # 3000 frames
3. Adjacent frames are highly correlated
correlation_coefficient ≈ 0.9 # typical inter-frame correlation
- Always remember to do Automatic checkpoint saving
- !pip install -U bitsandbytes>=0.41.0
- Put Your Teacher model on CPU
- MIN_DURATION = 1.0
- MAX_DURATION = 30.0 # Same as Whispe maximum acceptance length
Orignial LoRA Paper
ΔW = A · B -> only low-rank increments are made to W_q and W_v in the attention
Choices of LoRA Injection
decoder.layers.*.encoder_attn.q_proj
decoder.layers.*.encoder_attn.v_proj
decoder.layers.*.self_attn.q_proj
decoder.layers.*.self_attn.v_proj
decoder.layers.*.encoder_attn.q_proj, encoder_attn.k_proj, encoder_attn.v_proj
decoder.layers.*.self_attn.q_proj, self_attn.k_proj, self_attn.v_proj
decoder.layers.*.fc2
decoder.layers.*.encoder_attn.q_proj, encoder_attn.k_proj, encoder_attn.v_proj, encoder_attn.out_proj
decoder.layers.*.self_attn.q_proj, self_attn.k_proj, self_attn.v_proj, self_attn.out_proj
decoder.layers.*.fc1, fc2
Temperature
- Initial pilot temperature:
T = - Search range:
[ ] - Optuna hyperparameter: include
temp as a tunable parameter - Guidance: prevent over-smoothing (i.e. avoid
T > 5)
Hard vs. Soft Labels in Knowledge Distillation
-
Hard Labels: one-hot vectors from ground truth
y = [0, …, 1, …, 0]
• Strong supervision → binary certainty
• Forces correct classification
-
Soft Labels: teacher’s softmax outputs
p_teacher = [0.6, 0.3, 0.1]
• Confidence & uncertainty
• Encodes inter-class similarity
The num_workers parameter in PyTorch DataLoader controls the number of CPU processes responsible for data loading and preprocessing. This directly impacts GPU utilization through data pipeline optimization
Single-threaded (num_workers=0)
- CPU: Load→Preprocess→Transfer, GPU idle, Load→Preprocess→Transfer
- GPU: Idle, Compute, Idle
Multi-threaded (num_workers=4)
- CPU: Continuous data preparation (4 parallel threads)
- GPU: Continuous computation (minimal idle time)
Key Insight
- Increasing num_workers enhances “CUDA kernel parallelism” not by adding GPU parallelism, but by eliminating GPU starvation. Multiple CPU workers ensure the GPU receives a steady stream of preprocessed data, maximizing hardware utilization and reducing training time
- The optimal num_workers typically ranges from 2-4 per GPU, depending on CPU core count and I/O bottlenecks
CTC Loss - Hard Supervision - Here Cross-Entropy (CE) Loss since Whisper is Seq2Seq with Decoders
Since Whisper is a Seq2Seq model with Decoder, cross-entropy loss is employed here.
The decoder generates hidden state sequences at step $u$: \(\{\mathbf{d}_u\}_{u=1}^U\)
mapping to the target text sequence: \(\{y_u\}_{u=1}^U\)
using token-by-token one-to-one supervision:
- Token-to-Token Alignment Each step has a clear “correct” next token, requiring no implicit alignment
- One-Step Supervision Cross-entropy is directly applied to the prediction distribution at each position $u$
- Direct Gradient Backpropagated from the output layer, enabling stable convergence
Cross-Entropy Loss Formula \(\mathcal{L}_{\mathrm{CE}} = -\sum_{u=1}^U \log P_\theta\bigl(y_u \mid y_{<u}, \mathbf{h}_{1:T}\bigr)\)
where:
- $\mathbf{h}_{1:T}$ represents the audio representation output by the encoder
- $y_{<u}=(y_1,\dots,y_{u-1})$ are the previously generated tokens
- $U$ is the target sequence length
Following the encoder’s output audio frame sequence: \(\{\mathbf{h}_t\}_{t=1}^T\)
mapping to transcript tokens: \(\{y_u\}_{u=1}^U\)
without explicit frame-level labels:
- Frame-to-Token Alignment Automatic alignment from audio frames to text tokens
- Marginalizing Paths Marginalizing over all possible alignment paths
- Gradient Signal Gradient signals propagate to all relevant audio frames through attention mechanisms
KL Distillation Loss - Soft Supervision
KL Distillation Loss compares the teacher’s and student’s posterior distributions over labels at each time-step in latent space
- Soft Distribution Matching
- Preference Transfer
- Capturing Uncertainty
Since the softmax outputs retain probabilities for all tokens, the KL term transfers the teacher’s uncertainty patterns—e.g., when the teacher is unsure between two phonemes, the student learns to mirror that ambiguity
Total Loss
\[L_{\text{total}} = L_{\mathrm{CE}} + 0.xx\,T^{2}\,L_{\mathrm{KD}} + \alpha\,L_{\mathrm{hidden\_align}}\] where
\[\begin{aligned} & L_{\mathrm{CE}} &&\text{is the hard CE loss}\\ & L_{\mathrm{KD}} = \mathrm{KL}\bigl(p_{\rm teacher}^{T}\;\|\;p_{\rm student}^{T}\bigr) &&\text{is the softened KL-divergence loss with temperature }T\text{ and weight }\0.8 (*the same as student backbone)\\ & L_{\mathrm{hidden\_align}} &&\text{is the projected hidden-state MSE loss with weight }\alpha \end{aligned}\]
Hyperparameter Optimization
With 15hrs dataset experiment, we used 50 rounds to run a “warm-up” for no problem. If you want to perform large-scale tuning in a production environment, it is recommended to increase n_trials to 50-100
import optuna
from optuna.pruners import MedianPruner
from optuna.samplers import TPESampler
def objective(trial):
# Distillation loss weights
alpha = trial.suggest_loguniform("alpha", 1e-3, 1e1)
beta = trial.suggest_loguniform("beta", 1e-3, 1e1)
# Optimization hyperparameters
lr = trial.suggest_loguniform("lr", 1e-5, 1e-3)
batch_size= trial.suggest_categorical("batch_size", [4, 8, 16, 32])
dropout = trial.suggest_float("dropout", 0.0, 0.5)
# Train & evaluate with these settings (implement train_and_evaluate accordingly)
wer = train_and_evaluate(
alpha=alpha,
beta=beta,
learning_rate=lr,
batch_size=batch_size,
dropout=dropout,
pruner=trial # for early stopping
)
return wer
# Pruner to stop unpromising trials early
pruner = MedianPruner(n_startup_trials=5, n_warmup_steps=100)
sampler = TPESampler()
study = optuna.create_study(
direction="minimize",
sampler=sampler,
pruner=pruner
)
study.optimize(objective, n_trials=100)
print("Best hyperparameters:", study.best_params)
PCA vs. t-SNE vs. UMAP vs. DTW
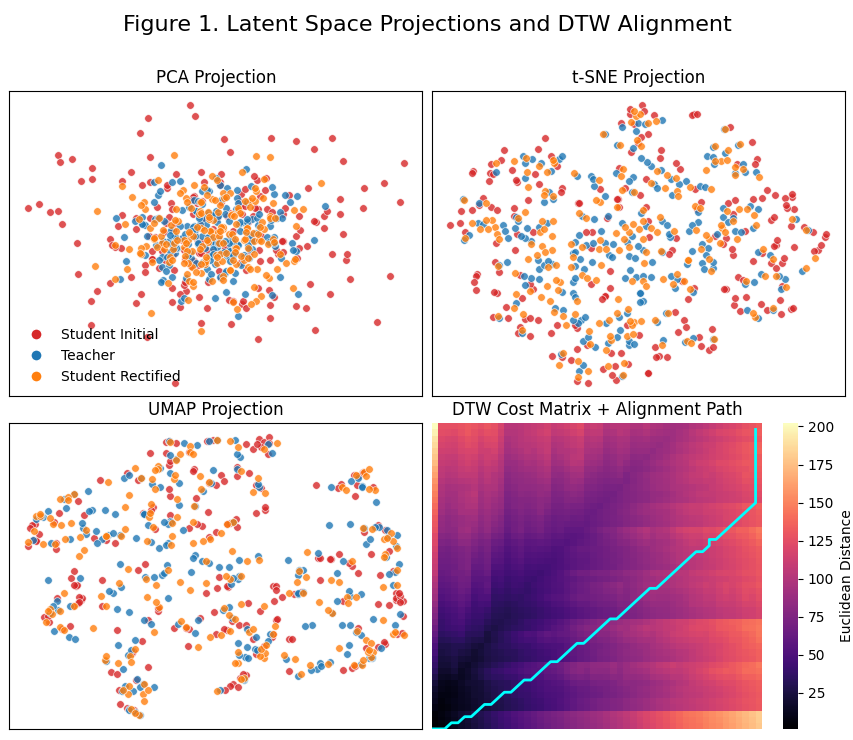
| Method | Category | Linear | Preserves | Mathematical Core | Typical Use Case |
| PCA | Dimensionality reduction | Yes | Global variance | Eigen-decomposition of covariance | Compression, noise reduction |
| t-SNE | Manifold learning | No | Local neighborhoods | KL divergence minimization | Visualization |
| UMAP | Manifold learning | No | Local + some global structure | Fuzzy simplicial sets | Visualization + clustering |
| DTW | Distance measure | No | Temporal alignment | Dynamic programming | Time-series similarity |
- Local weights
w_ij = exp(−(d(x_i, x_j) − ρ_i) / σ_i)
w_ji = exp(−(d(x_j, x_i) − ρ_j) / σ_j)
- Fuse into a single “strength” score
μ_ij = w_ij + w_ji − w_ij * w_ji
Background Knowledge 2
[Training Neural Network]
│
▼
[Problem: Overfitting]
│ model performs well on train set
└─ poor generalization on unseen data
▼
[Regularization Strategies]
│
├─ L1 Regularization → add |w| penalty
│ encourages sparsity, feature selection
│
├─ L2 Regularization (Weight Decay)
│ adds w² penalty, smooths weights
│ reduces variance, stabilizes gradients
│
├─ Early Stopping
│ monitor validation loss → stop early
│
├─ Data Augmentation
│ enlarge dataset (flip, crop, color jitter)
│ improves robustness & invariance
│
└─ Dropout
randomly deactivate neurons (mask m)
prevents co-adaptation
during inference: scale activations by p
▼
[Normalization Layers]
│
├─ Batch Normalization (BN)
│ normalize activations per mini-batch
│ μ_B, σ_B computed over batch samples
│ then apply γ (scale) + β (shift)
│ allows larger learning rate & faster training
│
├─ Layer Normalization (LN)
│ normalize across features, not batch
│ used in Transformers (batch-size independent)
│
└─ Effect:
stabilizes gradient flow
reduces internal covariate shift
improves convergence speed
▼
[Residual Connections]
│
└─ skip connection y = F(x) + x
eases gradient propagation
enables very deep CNNs (ResNet)
▼
[Combined Strategy]
│
├─ Regularization (L1/L2)
├─ Dropout
├─ Batch Normalization
└─ Data Augmentation
▼
[Result]
│
└─ High generalization, stable training,
smoother optimization landscape,
reduced overfitting risk
[Closed-Set Classification]
│
└─ assumes all test classes are known
model outputs one of O fixed labels
▼
[Open-Set Problem]
│
├─ real-world contains unknown categories
├─ standard SoftMax → overconfident wrong predictions
└─ need to reject unseen (unknown) samples
▼
[Goal: Open-Set Recognition]
│
├─ recognize known classes correctly
└─ detect / reject unknown classes (OOD)
▼
[Two Main Paradigms]
│
├─ Two-Stage OSR
│ Stage 1: detect unknowns (OOD)
│ Stage 2: classify known samples
│
└─ Integrated OSR
single model learns known + reject class
adds “unknown” logits or rejection threshold
▼
[Core Approaches]
│
├─ OSDN (Open-Set Deep Network)
│ compute Mean Activation Vector (MAV)
│ distance D_o = ||ϕ - μ_o||
│ fit EVT (Extreme Value Theory) model to tails
│
├─ GHOST (Gaussian Hypothesis OSR)
│ per-class Gaussian modeling in feature space
│ normalize logits by (μ_o, σ_o)
│ provides calibrated confidence
│
├─ Garbage / Background Class
│ add class y₀ for “none of the above”
│ weighted loss: λ_τ = N / ((O+1)N_τ)
│
├─ Entropic Open-Set Loss
│ for unknowns, enforce uniform SoftMax
│ target: t_o = 1/O for all o
│ equalizes logits → high entropy
│
└─ Confidence Thresholding
use ζ threshold on SoftMax
accept if max(ŷ_o) > ζ, else reject
▼
[Training]
│
├─ Known samples: one-hot targets
├─ Unknown samples: uniform targets
└─ Loss combines CE + Entropic term
▼
[Evaluation Metrics]
│
├─ CCR (Correct Classification Rate)
│ true positives among known samples
│
├─ FPR (False Positive Rate)
│ unknowns misclassified as knowns
│
└─ OSCR Curve (CCR vs FPR)
area under curve (AUOSCR) = performance
▼
[Modern Implementations]
│
├─ ImageNet-based OSR protocols (P1–P3)
├─ Feature-space Gaussian models (GHOST)
├─ Entropic loss + background class hybrid
└─ Evaluation by AIML UZH / WACV 2023
▼
[Outcome]
│
└─ OSR enables reliable recognition under uncertainty:
“I know what I know — and I know what I don’t.”
ResNet
Plain Net: ResNet:
Input Input
│ │
[Conv] [Conv]
│ │
[Conv] vs [Conv] +───┐
│ │ │
[Conv] [Conv] ◄──┘
│ │
Output Output
# Pooling Layer
Local region
┌───────────────┐
│ weak weak │
│ │
│ weak STRONG│ ──► STRONG
└───────────────┘
# 2D + 3D Convolution
Input: H × W × C
Kernel: k × k × C
Input: H × W × T × C
Kernel: k × k × k × C
| Stage | Process | Mathematical Meaning | Intuitive Explanation |
| Forward Process | Add Gaussian noise to clean trajectories \((x_0 \rightarrow x_T)\). | \(q(x_t \mid x_{t-1}) = \mathcal{N}(\sqrt{1 - \beta_t} \, x_{t-1}, \, \beta_t I)\) | Gradually “scrambles” a human driving path — this step is fixed and not learned. |
| Reverse Process | Learn to denoise noisy trajectories \((x_T \rightarrow x_0)\) conditioned on perception \(c\). | \(p_\theta(x_{t-1} \mid x_t, c) = \mathcal{N}(\mu_\theta(x_t, t, c), \Sigma_\theta)\) | The model learns to “restore order from noise,” reconstructing human-like trajectories that fit the scene. |
| Prior-Guided Learning | Add an Anchored Gaussian prior for realistic initialization. | \(x_T \sim \mathcal{N}(\mu_{anchor}, \sigma^2 I)\) | The model doesn’t predict trajectories directly—it learns to move toward the probability distribution of human driving behaviors. |
Temporal Alignment Leakage
┌─────────────────────────────────────────┐
│ Temporal Downsampling Effect │
│ │
│ Teacher Sequence (1500 frames) │
│ ┌─┬─┬─┬─┬─┬─┬─┬─┬─┬─┬─┬─┬─┬─┬─┬─┬─┬─┐ │
│ │▓│▓│▓│▓│▓│▓│▓│▓│▓│▓│▓│▓│▓│▓│▓│▓│▓│▓│ │
│ └─┴─┴─┴─┴─┴─┴─┴─┴─┴─┴─┴─┴─┴─┴─┴─┴─┴─┘ │
│ ↓ 3:1 compression │
│ Student Sequence (499 frames) │
│ ┌─────┬─────┬─────┬─────┬─────┬─────┐ │
│ │ ▓▓▓ │ ▓▓▓ │ ▓▓▓ │ ▓▓▓ │ ▓▓▓ │ ▓▓▓ │ │
│ └─────┴─────┴─────┴─────┴─────┴─────┘ │
│ ↑ │
│ Information "leaks" to adjacent windows│
└─────────────────────────────────────────┘
| Method | Memory Usage | Training Speed |
| Normal Training | High (store all activations) | Fast (no recomputation needed) |
| Checkpointing | Low (store partial activations) | Slow (extra recomputation needed) |
Gradient Checkpointing
Forward Pass:
Input → [Layer1: store] → [Layer2: recompute later] → [Layer3: recompute later] → Output
Backward Pass:
Recompute Layer2 & Layer3 forward
Use recomputed activations → compute gradient
Use Layer1 activation → compute gradient
Git Extended Workflow with Merge
| Step | Command | Purpose | Data Location |
| 1 | git add . | Stage modified files for the next commit. | Staging Area |
| 2 | git commit -m "..." | Record a new version snapshot. | Local Repository |
| 3 | git pull origin main | Fetch updates from the remote and merge them into your local branch. | Merges remote changes into Local Repository and Working Directory. |
| 4 | git push origin main | Upload local commits to the remote repository (e.g., GitHub). | Cloud (Remote Repository) |
ARM as Advanced RISC Machine
| Architecture | Typical devices | Instruction style | Power use | Example chips |
| ARM (aarch64 / ARM64) | Apple Silicon (M1, M2, M3), smartphones, tablets | RISC (Reduced Instruction Set Computer) | Very efficient | Apple M1, M2, Snapdragon, Raspberry Pi |
| x86 / x64 | Intel & AMD desktops/laptops | CISC (Complex Instruction Set Computer) | More power-hungry | Intel Core i7, AMD Ryzen |
Major CPU Architectures (with origin, purpose, and usage)
| Architecture | Type | Invented by | First Appeared | Core Idea | Typical Devices / Users | Status Today |
| x86 | CISC | Intel | 1978 (Intel 8086) | Large, complex instruction set for flexible programming and backward compatibility | Intel/AMD desktop & laptop CPUs | Still dominant in PCs and many servers |
| x86-64 (AMD64) | CISC (64-bit extension) | AMD | 2003 | Extended x86 to 64-bit while keeping backward compatibility | Modern Intel & AMD CPUs | Standard in all x86-based computers |
| ARM (AArch32/AArch64) | RISC | Acorn Computers / ARM Ltd. (UK) | 1985 | Small, fast, energy-efficient instruction set | Apple M-series, smartphones, tablets, embedded systems | Dominant in mobile and growing in PCs |
| PowerPC | RISC | IBM, Motorola, Apple (AIM Alliance) | 1991 | High-performance RISC for desktops and servers | Old Apple Macs (before 2006), IBM servers, game consoles | Still used in IBM high-end systems |
| MIPS | RISC | Stanford University (John Hennessy) | 1981 | “Minimal instruction set” design for simplicity and speed | Early workstations, routers, embedded devices | Mostly replaced by ARM and RISC-V |
| SPARC | RISC | Sun Microsystems | 1987 | Scalable RISC for servers and scientific computing | Sun servers, Oracle systems | Rarely used, mostly legacy |
| RISC-V | RISC (open-source) | UC Berkeley (Krste Asanović et al.) | 2010 | Fully open instruction set — anyone can implement it | Academic, open hardware, AI accelerators | Rapidly growing open standard |
| Itanium (IA-64) | VLIW (Very Long Instruction Word) | Intel & HP | 2001 | Parallel execution through compiler scheduling | Enterprise servers (HP/Intel) | Discontinued, considered a failed experiment |
| Alpha | RISC | Digital Equipment Corporation (DEC) | 1992 | 64-bit performance-focused RISC design | High-performance servers (1990s) | Discontinued after DEC acquisition by Compaq |
| VAX | CISC | Digital Equipment Corporation (DEC) | 1977 | Very rich and complex instruction set | Mainframes, early minicomputers | Historical only, inspired x86 and others |
GPU memory (HBM) vs CPU memory (DDR)
| Aspect | GPU Memory (HBM / HBM2e / HBM3) | CPU Memory (DDR4 / DDR5) |
| Physical location | On-package with GPU (2.5D interposer) | Off-chip DIMMs on motherboard |
| Primary purpose | Feed massively parallel compute units | Serve general-purpose workloads |
| Typical capacity per device | 16–80 GB (A100: 40/80 GB) | 64 GB – several TB per node |
| Scalability | Limited by package area and cost | Easily scalable via DIMM slots |
| Address space | Private to each GPU | Shared across all CPU cores |
| Latency | Higher than CPU cache, lower than PCIe | Lower than GPU HBM |
| Coherency | Not hardware coherent with CPU | Hardware cache coherence |
Memory bandwidth comparison
| Aspect | GPU HBM Bandwidth | CPU DDR Bandwidth |
| Typical peak bandwidth | 900–3000 GB/s | 100–400 GB/s |
| Bus width | Extremely wide (4096–8192 bit) | Narrow (64 bit per channel) |
| Number of channels | Many HBM stacks in parallel | 4–12 memory channels |
| Access pattern | Optimized for streaming and throughput | Optimized for low latency |
| Sustained bandwidth | Very high for regular access | Drops quickly under contention |
| Primary bottleneck | Bandwidth-bound kernels | Latency-bound workloads |
Why and How They Be Determined
| Dimension | Memory Capacity | Memory Bandwidth |
| Determined by | Number of DRAM cells | Number and width of data paths |
| Physical limiter | Silicon area, HBM stacks | Memory controllers, I/O pins |
| Can be “pooled” across devices | No | No |
| Helps with | Fitting models and activations | Feeding compute units fast enough |
| Typical failure mode | Out-of-memory | Compute units stall |
Memory Types in Hardware Hierarchy and Naming Context
| Name | Full Name | Hardware Layer | Attached To | Naming Basis | Primary Role |
| SRAM | Static Random Access Memory | On-chip cache (L1/L2/L3) | CPU / GPU | Storage mechanism | Low-latency cache to hide memory access delays |
| DRAM | Dynamic Random Access Memory | Main system memory | CPU | Storage mechanism | General-purpose working memory |
| DDR | Double Data Rate SDRAM | Main system memory | CPU | Signaling technique | High-throughput system memory |
| LPDDR | Low-Power Double Data Rate | Main memory (mobile) | CPU / SoC | Power optimization | Energy-efficient system memory |
| VRAM | Video Random Access Memory | Device-local memory (conceptual) | GPU | Intended use | GPU-attached working memory |
| GDDR | Graphics Double Data Rate | Device-local memory | GPU | Intended use + signaling | High-bandwidth graphics and compute memory |
| HBM | High Bandwidth Memory | Device-local memory | GPU / Accelerator | Bandwidth optimization | Extreme-bandwidth memory for accelerators |
Loss Functions in KD
| Loss Name | Mathematical Form | Purpose | Why | |
| Hard CE | $-\sum_i y_i \log q_i$ | Correctness | Prevents deviation from the task | |
| Soft CE | $-\sum_i p_i^{(T)} \log q_i^{(T)}$ | Knowledge transfer | Encodes class similarity structure | |
| $T^2$ scaling | $T^2,\mathcal{L}_{\text{soft}}$ | Scale stabilization | Keeps gradient magnitude consistent | |
| Logit L2 | $\sum_i \lVert z_i - v_i \rVert^2$ | Limiting case | High-temperature approximation | |
| KL divergence | $\mathrm{KL}(p^{(T)} , | , q^{(T)})$ | Unified view | Asymmetric teacher → student matching |
| Soft target regularization | implicit | Regularization | Data-dependent prior from teacher | |
KD, BYOL, and Self-Distillation
| Loss / Objective | Who proposed | Why (English) |
| Hard Cross Entropy | Standard supervised learning (Shannon; modern deep learning) | To train models to predict the ground-truth label directly |
| Soft Cross Entropy (Soft Targets) | Hinton et al., 2015 | To transfer the teacher’s full output distribution, not just the argmax |
| Temperature $T$ | Hinton et al., 2015 | To expose dark knowledge encoded in low-probability classes |
| $T^2$ Gradient Scaling | Hinton et al., 2015 | To keep gradient magnitudes consistent when changing $T$ |
| Logit L2 Loss | Caruana et al., 2006 | To match teacher and student pre-softmax representations |
| KL Divergence View | Kullback–Leibler (1951), applied by Hinton et al. | To formalize distillation as asymmetric distribution matching |
| Soft Targets as Regularization | Hinton et al., 2015 (implicit) | To act as a data-dependent prior that reduces overfitting |
| BYOL Loss (Prediction Matching) | Grill et al., 2020 (BYOL) | To match representations between online and target networks without negative samples |
| Self-Distillation (EMA Teacher) | Mean Teacher (2017); BYOL (2020) | To distill knowledge from a temporally averaged version of the same model |
| Representation Consistency Loss | Self-distillation / BYOL line of work | To enforce invariance across views, augmentations, and training time |
L2 Loss vs. Geodesic Loss
| L2 Loss | Geodesic Loss |
| Euclidean space | Curved (Riemannian) space |
| Sensitive to vector norm | Depends only on direction |
| Encourages radial collapse | Avoids radial degeneration |
Point vs. Curve Distillation
| Dimension | Point (main experiment) | Curve (ablation 2) |
| Basic object | Single hidden state | Sequence of hidden states |
| Mathematical object | Vector | Vector-valued function |
| Geometric structure | Point on a hypersphere | Curve on a hypersphere |
| Loss operates on | Point-to-point alignment | Local shape + global discrimination |
| Order sensitivity | No | Yes |
| Second-order information | No | Yes (curvature) |
| Aspect | Point Alignment (main experiment) | Curve Alignment (ablation 2) |
| Geometric object | Point on a hypersphere | Curve on a hypersphere |
| Mathematical form | Vector | Vector-valued function |
| What is matched | Representation position | Representation evolution |
| Temporal dependency | Ignored | Explicitly modeled |
| Loss acts on | Individual states | Local shape + global structure |
| Information order | Zero-order (state) | First/second-order (velocity, curvature) |
| Constraint strength | Weak | Strong |
| Optimization behavior | Stable | Sensitive |
| Overfitting risk | Low | Higher |
| Information density | Coarse | Very high |
| Essential meaning | Semantic alignment | Process / trajectory alignment |
Distillation Methods and Who Proposed
| Distillation Type | Who Proposed | Brief Description |
| Logit Distillation | Caruana et al., 2006 (model compression) and early KD literature | Directly matches teacher and student logits (pre-softmax values) using e.g. L2 loss on logits |
| Label (Soft-Label) Distillation | Hinton et al., 2015 (“Distilling the Knowledge in a Neural Network”) | Matches teacher and student softmax probability distributions (soft targets) using cross-entropy / KL divergence |
ODE, SDE, and Neural ODE
| Aspect | ODE (Ordinary Differential Equation) | SDE (Stochastic Differential Equation) | Neural ODE |
| Historical motivation | Describe deterministic physical laws | Model intrinsic randomness in dynamical systems | Learn continuous-time dynamics from data |
| When introduced | 17th century | 1940s | 2018 |
| Original problem | Predict future state from current state | Predict distributional evolution under noise | Replace discrete deep layers with continuous dynamics |
| Core equation | $ \frac{dx}{dt} = f(x,t) $ | $ dX_t = b(X_t,t),dt + \sigma(X_t,t),dW_t $ | $ \frac{dx}{dt} = f_\theta(x,t) $ |
| Nature of dynamics | Deterministic | Stochastic | Deterministic but learned |
| Role of randomness | None | Essential (Brownian noise) | None in dynamics (data-driven uncertainty only) |
| What evolves | A single trajectory | A distribution over trajectories | A trajectory parameterized by a neural network |
| Output interpretation | One future path | A family of possible paths | Continuous-depth transformation |
| Mathematical object | Function | Stochastic process | Neural-parametrized ODE |
| Relation to probability | Implicit (via initial condition) | Explicit (distribution is primary object) | Implicit; often paired with likelihood or flow models |
| Typical use cases | Physics, mechanics, control | Diffusion, Langevin dynamics, finance | Continuous normalizing flows, deep learning models |
| Key conceptual role | Deterministic time evolution | Distributional time evolution | Learnable continuous-time computation |
| Limiting relationship | — | Reduces to ODE when noise $\to 0$ | ODE with learned vector field |
| Existence & uniqueness | Picard–Lindelöf theorem: if $f$ is continuously differentiable with bounded derivatives (or more generally Lipschitz), a unique solution to the ODE exists; equivalently, a flow map exists | Existence & uniqueness theorem for SDEs: if $b$ is Lipschitz and $\sigma$ is continuous (or Lipschitz), a unique solution to the SDE exists | Inherits ODE guarantees under the same regularity assumptions on $f_\theta$ |
ODEs (Picard–Lindelöf theorem)
- If the vector field $f$ is Lipschitz (e.g., continuously differentiable with bounded derivatives), then a unique solution to $ \frac{dx}{dt} = f(x,t) $
- exists. Equivalently, a flow map is well-defined
SDEs (Existence and Uniqueness Theorem)
- If the drift $b$ is Lipschitz and the diffusion coefficient $\sigma$ is continuous (or Lipschitz), then a unique solution to $ dX_t = b(X_t,t),dt + \sigma(X_t,t),dW_t $
- exists
Key takeaways
- In the cases of practical interest for machine learning, unique solutions exist for both ODEs / flows and SDEs Stochastic calculus perspective
- Solutions to SDEs are constructed via stochastic integrals, defined as limits of Itô–Riemann sums
Sources of Non-Determinism in Training
| Concept | What it is | Who / Origin | When | Why it exists |
| RNG (Random Number Generator) | A mechanism that produces pseudo-random numbers controlling stochastic processes in training (e.g., data order, dropout, sampling). | Computer science & statistics community (e.g., Knuth); implemented in PyTorch, NumPy, CUDA | 1960s (theory); 2016+ in modern DL frameworks | Enables stochastic optimization, regularization, and scalable training over large datasets. |
| JIT Compilation | Just-In-Time compilation that generates optimized GPU kernels at runtime based on actual tensor shapes and hardware. | NVIDIA (CUDA), LLVM, adopted by PyTorch, cuDNN | ~2007 (CUDA); widely used in DL since ~2017 | Achieves hardware-specific performance without requiring precompiled kernels for every configuration. |
| Autotuning | Runtime benchmarking and selection of the fastest kernel among multiple implementations. | NVIDIA cuDNN / cuBLAS | ~2014–2016 | Maximizes throughput by adapting to input shapes, memory layout, and GPU architecture. |
Score Field Instead of Raw Data Distribution
| Representation | Requires normalization | Local / Global | Directly enters dynamics | High-dimensional feasibility |
| $p(x)$ | Yes | Global | No | No |
| $\log p(x)$ | Yes | Global | No | No |
| Energy $E(x)$ | No | Global | No | Limited |
| Score $\nabla_x \log p(x)$ | No | Local | Yes | Yes |
References




